Category: "mathematics"
Deprecated: Function create_function() is deprecated in /hermes/bosnacweb09/bosnacweb09ao/b2085/d5.hiro/public_html/PHP/b2evolution/inc/_core/_url.funcs.php on line 817
Deprecated: Function create_function() is deprecated in /hermes/bosnacweb09/bosnacweb09ao/b2085/d5.hiro/public_html/PHP/b2evolution/inc/_core/_url.funcs.php on line 818
Another explanation of what physics is with a little different perspective
November 22nd, 2016 Posted by Hiro Filed under education, mathematics, physics, science
Deprecated: Array and string offset access syntax with curly braces is deprecated in /hermes/bosnacweb09/bosnacweb09ao/b2085/d5.hiro/public_html/PHP/b2evolution/plugins/_auto_p.plugin.php on line 502
Deprecated: Array and string offset access syntax with curly braces is deprecated in /hermes/bosnacweb09/bosnacweb09ao/b2085/d5.hiro/public_html/PHP/b2evolution/plugins/_auto_p.plugin.php on line 500
Deprecated: Array and string offset access syntax with curly braces is deprecated in /hermes/bosnacweb09/bosnacweb09ao/b2085/d5.hiro/public_html/PHP/b2evolution/plugins/_texturize.plugin.php on line 116
Speaking of physics, people say, “It’s too hard to learn.”; “I don’t understand anything."; or "This is the theory that forms the basis of all technologies." They are right, but it does not seem that most people grasp what physics really is.
A long time ago, my friend said to me, “Mathematics makes sense to me, but it doesn’t make sense when it comes to physics, though they look similar ..." I was interested to notice that what other people think about physics is different from what we, physicists, think.
So I hope I can explain about physics with a slightly different perspective for this article.
There is a difference between mathematics and physics. A mathematical theory is a world created by mathematicians with very precise logic. On the other hand, for physics, nature or universe is the world and physicists try to explain how it works.
In other words, physicists construct a predictable theory using any means, such as experiments and mathematics, so we can understand how things move in nature. In that sense, it is impossible to completely prove the theory of physics, unlike mathematics.
However, physics is certainly an extremely robust empirical theory because many researchers have challenged it with many aspects, and physics still survives.
Most people who feel that physics is difficult don’t see the sense of "following nature's choice", I guess.
Also, some of people who study literature said, “The curriculum of physics is the same for the freshman, the sophomore, the junior, and senior. Don’t the students learn any new things in each year?”
This is the fact that the physics students have to learn the same subjects repeatedly even in the graduate school, such as, mechanics, electromagnetism, thermal and statistical mechanics, and quantum mechanics. But the contents for each year are obviously different.
Basic principles and equations are of course the same, but as each grade progresses, we have to deal with more complicated problems. If it gets complicated, the students have to learn more advanced mathematics and the abstract concepts. Therefore, it is hard for students to master the specific subject in one or two years.
Although it is true for other natural sciences and mathematics, physics requires accurate processes as important as the accurate final result. This is because if the conditions change, it will give us a completely different answer. But there is also other reason.
The process or the way of solving is also an invention of a very important tool for physics.
Some people say, "If you get the same answer anyway, you can use any method you like." However, by using a different method, we can check various things. In addition, we might solve other problem settings we could not even attempt before.
Hope you would appreciate the role of physics, natural sciences and mathematics, which each discovery or invention is very important and influential to the entire theory.
Photo credit: Stuck in Customs via Visual Hunt / CC BY-NC-SA
Deprecated: Function create_function() is deprecated in /hermes/bosnacweb09/bosnacweb09ao/b2085/d5.hiro/public_html/PHP/b2evolution/inc/_core/_url.funcs.php on line 817
Deprecated: Function create_function() is deprecated in /hermes/bosnacweb09/bosnacweb09ao/b2085/d5.hiro/public_html/PHP/b2evolution/inc/_core/_url.funcs.php on line 818
Can the sum of interior angles of a triangle be more than or less than 180 degrees?
September 19th, 2016 Posted by Hiro Filed under education, mathematics, technology, physics
What is the sum of the interior angles of a triangle? Most of people would answer 180 degrees, but physicists and mathematicians want to point out something with the question and answer.
Normally, if you draw a triangle on a paper, then the sum of three angles must be 180 degrees.
This is not an accurate description, but the geometry on a flat plane is called the Euclidean geometry. For instance, “parallel lines do not intersect" is one of the statements included in this geometry.
Now, what will happen if it is not on a flat plane? Namely, if you draw a figure on a curved surface, you may encounter some results which are not our commonsense. Such geometry is known as a non-Euclidean geometry.
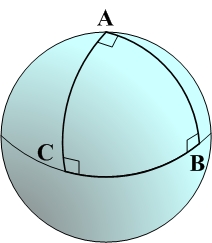
A typical example is a sphere. So let's imagine drawing a figure on the surface of the Earth. For humans’ point of view, it looks a flat plane on the Earth. However, it is a sphere macroscopically.
Let's start with the North Pole A in the figure. Draw a line straight down to the equator. Then, change the direction at the intersection B with a right angle. Keep drawing a straight line along with the equator. The distance should be one forth of the circumference of the circle made with the equator until point C. Finally, change the direction with a right angle, and draw a straight line toward the North Pole as shown in the figure.
You can see a large triangle on the Earth; then, look at each angle. The angles of B and C are 90 degrees, respectively. In this example, the angle A is also 90 degrees.
Therefore, the sum of the interior angles of the triangle becomes 270 degrees. In other words, the sum of the interior angles of a triangle in non-Euclidean geometry is not necessarily equal to 180 degrees.
In fact, this geometry is used for Einstein's theory of general relativity. The mass of stars deforms the space, and light goes on the curved surface. Thus, you have to take the above discussion into account to describe such mechanism.
Simply put, the general theory of relativity reinterprets the dynamics as the strength of gravity equivalent with the curvature of space.
Speaking of relativity, it still sounds like a scientific fiction. However, the Global Positioning System (GPS) is an application of the theories of relativity, and GPS could not be made without such modern theories of physics.