Research Plans
- My Previous Research Works
- My postdoctoral works are extended to three fields: (1) [Materials Science] We investigated an electronic structure by using an optimization program, such as maximum entropy principle. The method is one of inverse problems to re-construct a most-likely result from an incomplete set of data. This mathematical method can also be utilized for other fields, such as biological phenomena, medical data, sociological behaviors, etc. (2) [Mathematical Physics] Quantum theory can be re-considered with Parity-Time (PT) symmetric Hamiltonian. The Hamiltonian must be Hermitian so the eigen values become real; however, the PT symmetric Hamiltonian also can realize the real eigen values when the symmetry is unbroken. We investigated the properties and possible applications. (3) [Physics Education] Strategically utilizing educational methods in teaching introductory physics can reveal students' real understanding. Constructing curricula must be considered as dynamism of methods under students' comprehension. I investigated the strategy to implement possible curricula.
- My Ph.D. work is to construct the nucleon-nucleon (NN) potential with an innovative idea -- chiral effective field theory. [Nuclear Particle Physics] The traditional and famous potential is called meson exchange models (pion, etc.). Although you can obtain accurate results with meson exchange models, the theory itself is ad hoc.
- My BS work is to elaborate an efficient algorithm toward non-linear physical systems (pendulum, fluid dynamics, etc.). [Non-lenear and Chaotic Physics] The non-linear systems are not straightforward to analyze, and are recognized as non-integrable systems as the discussion of dynamical system. Therefore, a numerical solution is necessary. Obtaining an accurate result needs higher order numerical solutions. In addition, if the system is energy-conservative, one can use the symplectic method to eliminate the related accumulative error. We tested and developed the algorithms.
- Future Research Goals
- The future research is to develop applications to be extracted from the above research. (1) Medical physics: I want to investigate very low energy (about 50-150 MeV), which is used for the proton beam therapy, etc. Some non-linear implementation may lead to a new application. (2) Solid state physics: Extending nuclear physics to future ideas of the materials science will be considered. There are a lot of applications related to nuclear engineering. Many-body and complicated systems can be analyzed with several optimization programs. In addition, a time-dependent model can be considered in scattering with a beam in nuclear states. It will be important to discuss interesting properties for beam physics.
- A different perspective is to investigate the mathematical and computational properties of the nuclear potential. (1) Semi-classical analysis: The potential is highly non-linear (see the 2nd figure). Thus, to consider the semi-classical region, it will be a new topic (chaos in nuclear region). (2) Algorithm development: I also want to investigate some sensitivity of the potential since I did not use higher order accuracy for the part of the program. I will develop this with different algorisms to seek better computational insights, such as ant colony, genetic algorithm, neural network, etc. I also want to develop material and nuclear systems with random process (quantum walks) and continuum sense. (3) Mathematical development: PT symmetric Hamiltonian of nuclear and other solid-state potentials will surely be interesting to analyze. The above will be beneficial for the computational and mathematical progress in physics.
- For physics education, I have two main future projects. (1) Online Physics Lab: This project to implement the software so the students can experience the lab. Unlike the usual simulation, it includes error analyses and other possible mistakes in measurements. It will be beneficial for a distance education, which does not often have the lab part. (2) Establish Teaching and Learning Evaluation: Current evaluations are often subjective. I want to establish the evaluation system with mathematical methods, such as Bayesian statistics, etc. This evaluation will also involve the curriculum implementation to be effective.
- My Idea of How to Involve Students into Research
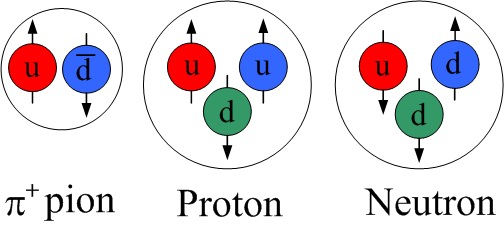
The above three particles are important for the NN interactions, and those consist of "up" and "down" quarks. The theory between quarks is called quantum chromo dynamics (QCD). Therefore, the NN interaction should fundamentally be explained in terms of QCD. The problem is that QCD is for only the high energy regime (so useless for the interaction between protons, neutrons, etc.). The chiral effective field theory provides a connection between QCD and nuclear physics. The specific method is called chiral perturbation theory (ChPT). I developed the NN potential energy with ChPT.

I would like to focus on following things:
(1) Selection of students: I will find the students who are curious, inquisitive, diligent, etc. and who will keep the attractiveness of my research activities.
(2) Group structure: I want to assemble one group of students with a range of experience, and another group of students who will continue in the group for several years. I also have to care about students' understanding of research, leadership development, research productivity, and mentoring time.
(3) Individual mentoring: I want to motivate students who show little independent initiative, encourage students who are frustrated by a project that fails, advise students of unrealistic expectations of research, and train students to maintain careful analyses and records.