Can the sum of interior angles of a triangle be more than or less than 180 degrees?
Deprecated: Array and string offset access syntax with curly braces is deprecated in /hermes/bosnacweb09/bosnacweb09ao/b2085/d5.hiro/public_html/PHP/b2evolution/plugins/_auto_p.plugin.php on line 502
Deprecated: Array and string offset access syntax with curly braces is deprecated in /hermes/bosnacweb09/bosnacweb09ao/b2085/d5.hiro/public_html/PHP/b2evolution/plugins/_auto_p.plugin.php on line 500
Deprecated: Array and string offset access syntax with curly braces is deprecated in /hermes/bosnacweb09/bosnacweb09ao/b2085/d5.hiro/public_html/PHP/b2evolution/plugins/_texturize.plugin.php on line 116
What is the sum of the interior angles of a triangle? Most of people would answer 180 degrees, but physicists and mathematicians want to point out something with the question and answer.
Normally, if you draw a triangle on a paper, then the sum of three angles must be 180 degrees.
This is not an accurate description, but the geometry on a flat plane is called the Euclidean geometry. For instance, “parallel lines do not intersect" is one of the statements included in this geometry.
Now, what will happen if it is not on a flat plane? Namely, if you draw a figure on a curved surface, you may encounter some results which are not our commonsense. Such geometry is known as a non-Euclidean geometry.
A typical example is a sphere. So let's imagine drawing a figure on the surface of the Earth. For humans’ point of view, it looks a flat plane on the Earth. However, it is a sphere macroscopically.
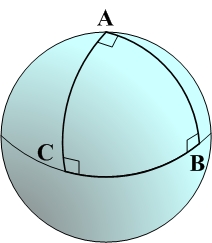
Let's start with the North Pole A in the figure. Draw a line straight down to the equator. Then, change the direction at the intersection B with a right angle. Keep drawing a straight line along with the equator. The distance should be one forth of the circumference of the circle made with the equator until point C. Finally, change the direction with a right angle, and draw a straight line toward the North Pole as shown in the figure.
You can see a large triangle on the Earth; then, look at each angle. The angles of B and C are 90 degrees, respectively. In this example, the angle A is also 90 degrees.
Therefore, the sum of the interior angles of the triangle becomes 270 degrees. In other words, the sum of the interior angles of a triangle in non-Euclidean geometry is not necessarily equal to 180 degrees.
In fact, this geometry is used for Einstein's theory of general relativity. The mass of stars deforms the space, and light goes on the curved surface. Thus, you have to take the above discussion into account to describe such mechanism.
Simply put, the general theory of relativity reinterprets the dynamics as the strength of gravity equivalent with the curvature of space.
Speaking of relativity, it still sounds like a scientific fiction. However, the Global Positioning System (GPS) is an application of the theories of relativity, and GPS could not be made without such modern theories of physics.