Category: "technology"
Deprecated: Function create_function() is deprecated in /hermes/bosnacweb09/bosnacweb09ao/b2085/d5.hiro/public_html/PHP/b2evolution/inc/_core/_url.funcs.php on line 817
Deprecated: Function create_function() is deprecated in /hermes/bosnacweb09/bosnacweb09ao/b2085/d5.hiro/public_html/PHP/b2evolution/inc/_core/_url.funcs.php on line 818
Fallacies of computer topics: A physicist's point of view II
December 6th, 2016 Posted by Hiro Filed under education, engineering, technology, physics
Deprecated: Array and string offset access syntax with curly braces is deprecated in /hermes/bosnacweb09/bosnacweb09ao/b2085/d5.hiro/public_html/PHP/b2evolution/plugins/_auto_p.plugin.php on line 502
Deprecated: Array and string offset access syntax with curly braces is deprecated in /hermes/bosnacweb09/bosnacweb09ao/b2085/d5.hiro/public_html/PHP/b2evolution/plugins/_auto_p.plugin.php on line 500
Deprecated: Array and string offset access syntax with curly braces is deprecated in /hermes/bosnacweb09/bosnacweb09ao/b2085/d5.hiro/public_html/PHP/b2evolution/plugins/_texturize.plugin.php on line 116
Another misunderstanding is as for the programming language, Fortran. This is one of the very old languages developed for numerical calculation of physics and mathematics, but still exists.
Fortran is a language specialized only for calculation, so it has been updated with such objective. In other words, Fortran becomes the most accurate and the quickest to calculate physics problems.
However, C language (later extended to C++) emerged in the market and it has been more versatile, especially for software engineers. Then, the language spread out for almost all the programmers.
After that, speaking of Fortran, people say, "You are still using such an old fossil-like language?", or "You can’t get any job if you use such a language."
Indeed, most of those people have never used Fortran, and they do not even have programming experiences. (By the way, I have used two languages, C / C++ and Fortran, in the calculation of physics and mathematics for a long period.)
Currently, Fortran is still being developed. Related engineers are upgrading it so that we can even use pointers and object oriented programming, which could only be used in C /C++ a long time ago. On the other hand, for C/C++, people created a lot of libraries and modules for numerical calculation. Now, the difference between Fortran and C has decreased.
However, there are still some weak points for each of them. Fortran cannot be used as a general purpose. In other words, Fortran is still not optimized as a role of programming the software. (Maybe, it doesn’t have to be…)
Then, C / C++ has a weakness in giving accurate numerical values. The default accuracy of Fortran is much better than C /C++.
A couple of years ago (about year of 2014), I had to give numerical values using the formula of quartic equation, which is called Ferrari's formula. I initially used C, but the result was far from the exact solution. Then, I programmed the same algorithm with Fortran, and as a result, I was able to get the accurate values that were very close to the exact solutions.
I believe that the computer and its languages will be developed further in the future. Thus, rather than learning only a popular language, people should master multiple languages and spend a time to accomplish something with those programming languages. That will be more important as a programmer or a simulator.
Deprecated: Function create_function() is deprecated in /hermes/bosnacweb09/bosnacweb09ao/b2085/d5.hiro/public_html/PHP/b2evolution/inc/_core/_url.funcs.php on line 817
Deprecated: Function create_function() is deprecated in /hermes/bosnacweb09/bosnacweb09ao/b2085/d5.hiro/public_html/PHP/b2evolution/inc/_core/_url.funcs.php on line 818
Fallacies of computer topics: A physicist's point of view I
December 5th, 2016 Posted by Hiro Filed under education, engineering, technology, physics
As a physicist, I have had many opportunities to use computers. My job has involved managing hardware and software for physics experiments, programming for numerical calculation, and repairing of system problems.
However, I am not a computer expert. I don’t have a degree of computer science. I don’t have experience in developing computer software either. So you can see I am a person between computer amateurs and the experts. In this article, I would like to point out fallacies related computer topics as a physicist.
First of all, for people who do not know computers much, the concept of bits is not well understood. A common mistake is that "64 bits is twice the 32 bits."
A bit is a unit for counting the number of digits in the binary number system. Therefore, one bit is one digit, which represents two ways such as 0 and 1. If you have 2 bits, it will be four ways with two digits and each with two ways.
By considering this rule, we conclude 32 bits as 2 to the power of 32 ways. So 64 bits are as 2 to the power of 64. Therefore, 64 bits will be 4294967296 times larger than 32 bits. (You can simply calculate 264 divided by 232.)
Certainly, the number of digits is twice, but from the number of cases it can handle, this value is more meaningful to consider the power of computation.
This is the same as physics. The units represent what the numbers are, and give you the meaning.
Picture by by John Kovacich
Deprecated: Function create_function() is deprecated in /hermes/bosnacweb09/bosnacweb09ao/b2085/d5.hiro/public_html/PHP/b2evolution/inc/_core/_url.funcs.php on line 817
Deprecated: Function create_function() is deprecated in /hermes/bosnacweb09/bosnacweb09ao/b2085/d5.hiro/public_html/PHP/b2evolution/inc/_core/_url.funcs.php on line 818
Can the sum of interior angles of a triangle be more than or less than 180 degrees?
September 19th, 2016 Posted by Hiro Filed under education, mathematics, technology, physics
What is the sum of the interior angles of a triangle? Most of people would answer 180 degrees, but physicists and mathematicians want to point out something with the question and answer.
Normally, if you draw a triangle on a paper, then the sum of three angles must be 180 degrees.
This is not an accurate description, but the geometry on a flat plane is called the Euclidean geometry. For instance, “parallel lines do not intersect" is one of the statements included in this geometry.
Now, what will happen if it is not on a flat plane? Namely, if you draw a figure on a curved surface, you may encounter some results which are not our commonsense. Such geometry is known as a non-Euclidean geometry.
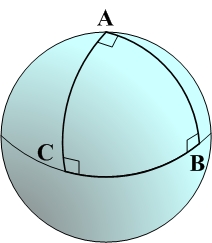
A typical example is a sphere. So let's imagine drawing a figure on the surface of the Earth. For humans’ point of view, it looks a flat plane on the Earth. However, it is a sphere macroscopically.
Let's start with the North Pole A in the figure. Draw a line straight down to the equator. Then, change the direction at the intersection B with a right angle. Keep drawing a straight line along with the equator. The distance should be one forth of the circumference of the circle made with the equator until point C. Finally, change the direction with a right angle, and draw a straight line toward the North Pole as shown in the figure.
You can see a large triangle on the Earth; then, look at each angle. The angles of B and C are 90 degrees, respectively. In this example, the angle A is also 90 degrees.
Therefore, the sum of the interior angles of the triangle becomes 270 degrees. In other words, the sum of the interior angles of a triangle in non-Euclidean geometry is not necessarily equal to 180 degrees.
In fact, this geometry is used for Einstein's theory of general relativity. The mass of stars deforms the space, and light goes on the curved surface. Thus, you have to take the above discussion into account to describe such mechanism.
Simply put, the general theory of relativity reinterprets the dynamics as the strength of gravity equivalent with the curvature of space.
Speaking of relativity, it still sounds like a scientific fiction. However, the Global Positioning System (GPS) is an application of the theories of relativity, and GPS could not be made without such modern theories of physics.